SD法是以现代数学地质为基础的动态分维拓扑学理论的中国自主资源储量估算方法体系，有别于前苏联体系的传统简单几何学原理和欧美体系的概率统计数学原理，于20世纪末由我国地质科技工作者唐义和蓝运蓉在地质找矿、矿产资源勘查实践中运用数学与计算机为工具共同创立。SD法具有理论、原理、方法等方面的含义，分别代表“Spline”样条函数和“动”态分维；代表“搜”索、“递”进；代表“审定（即：对资源储量精确程度的定量确定）”。SD法体系主要分为SD储量计算法和储量审定法（SD精度），还包括四条原理（“降维形变原理”、“权尺稳健原理”、“搜索求解原理”和“递进逼近原理”）、八组公式（SD稳健公式、结构地质变量公式、SD边值公式、SD复杂度公式、SD风暴品位下限值公式、SD样条函数公式、SD体积公式、SD精度公式）及系列软件（单机版本、企业网络版本和现代移动互联网版本）。

A.1 定量确定矿体复杂度

       为了能比较准确描述矿体的复杂程度，SD法引入了动态分维理论，并提出了品位复杂度和厚度复杂度的概念，这两个概念是适合矿体特性和要求，从动态分维角度来精细地刻画和描述矿体复杂程度。它充分考虑了地质变量的空间结构性特点，包括工程品位、厚度的大小，工程所处的位置及工程间的距离等。

       矿体复杂度分品位复杂度Tc和厚度复杂度Th以及矿体的综合复杂度Tz，用以定量描述矿体的复杂程度。复杂度在[0,1]之间，是矿体复杂程度的最终衡量参数，具体表达通式如下：

                                                                                       (1)

                                                                                        (2)

                                                                                            (3)    

                                                                     (4)

                                                                                                              (5)

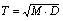
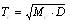
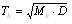
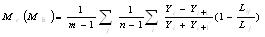
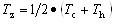
            T_c——矿体品位复杂度；

            T_h——矿体厚度复杂度；

            T_z——矿体综合复杂度及T；

            M_c——品位变化度；

            M_h——厚度变化度；

            D ——SD分数维；

            m ——线数。

              j ——线的序号，j=1.2. … m；

             n ——点数；

              i ——观测点序号，i=1.2.… n；

            Yi ——观测点的观测值（单工程的平均品位或厚度值）；

             Lij ——小区间距离：；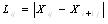

             Lj ——j线I个区间总距离：；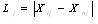

       SD法对矿体复杂度（厚度复杂度、品位复杂度、综合复杂度）按照复杂程度进行了五级定量划分标准，具体应用中均以此为标准：

       a) 简  单： 0～0.0625

       b) 较简单： 0.0625～0.25

       c) 一  般： 0.25～0.39

       d) 较复杂： 0.39～0.56

       e) 极复杂： 0.56～1

A.2 风暴品位处理

       风暴品位的存在是客观的，它的出现会影响平均品位的可靠性。SD法不去寻求原始数据的统计规律，而用稳健处理数据的方法，将原始数据处理成相对平滑的空间结构的数据，即结构地质变量，但是，SD法仍然要求结构数据的合理性即合理均值。为排除特异值对结果正确性干扰，SD法对它进行了稳健性处理。

       SD法采用修匀数据的办法来消减风暴品位在参与计算时过大的影响力，从而达到计算结果稳健可靠的目的。SD法处理风暴品位值的办法是，将风暴品位值适度削减，将削减值替代风暴值，置于原始数据中参与计算。风暴品位处理具体公式：

                                                                                                                                   (6)

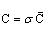
       (6)式中：

         C ——风暴品位下限值；

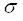
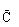
       ——风暴品位倍数限；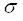

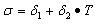
        ——采用搜索法计算的矿体平均品位。

        风暴品位倍数限计算公式：

                                                                                                                     (7)

       (7)式中：

       δ1 ——截距常数2.933；

       δ2 ——斜率常数17.067。

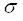
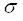
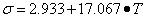
       可见，是矿体复杂度T的函数。又可写成另一形式：

                                                                                                       (8)

       用风暴品位作为替代值符合矿体变化规律，在适度削减其过大影响权力的同时，仍然能保持其风暴值的优势，避免了目前特高品位处理过程中过多削减特高值而违背地质规律的不合理现象。

A.3 风暴厚度处理

       风暴厚度是指计算中单工程厚度呈现出的风暴值。

       风暴厚度的判别依据：首先将全区单工程厚度从小到大排序后，位于序尾、比例一般不超过3%～5%的区域，作为风暴厚度可疑区，在可疑区内，当SD样条曲线出现强烈震荡，以致出现负值现象时或未出现震荡且单工程厚度大于矿区平均厚度的3倍时，确定为风暴厚度。

       风暴厚度和风暴品位不同，风暴品位是以点带面，风暴厚度是以线带面，SD三次样条上表现为成规模性，若直接改变单工程的厚度值则不符合SD样条曲线对客观情况的体现，因此，不应改变风暴厚度值，只有当控制程度较低且出现风暴厚度时，适当考虑缩小其影响范围。

A.4 确定SD外推边值

A.4.1 这里的外推范围主要指边缘见矿工程以外的无限外推；外推距离的确定建议按照SD法原则并结合矿床具体情况设置。

A.4.2 外推距离的合理设置一般为：SD基距或“探明的”框棱。SD基距相当于SD精度接近100%时（矿体完全查明，接近真态）的工程控制间距（框棱）。这里“探明的”框棱有两个含义，一个是通常相当于SD精度≥80%时的工程控制间距，称之为“确定探明的”框棱，另一个是，实际应用中，由待定区间归属后的“归属探明的”框棱（SD精度为65%～80%）；

A.4.3 外推距离设置的基本原则是“若工程控制范围内的地质认识较清楚，则允许适当多推，否则，应少推”。一般地，高勘查程度（详查以上）可以取上限值的高值（即：“归属探明的”框棱），低勘查程度允许取上限值的低值（即：“确定探明的”框棱），对于单孔控矿的情况，建议取下限值（SD基距）。

A.4.4 对于外推值的合理推断是影响资源储量结果不可忽视的一个主要问题，一个合理的外推模型要与矿床变化规律紧密结合，SD法就是根据矿床成因类型紧扣变化规律进行外推范围的推测，而且非等值外推，可能比边缘见矿工程厚大还大，也可能小。具体外推公式如下：

                                                                                           (9)

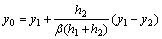
       (9) 式中：

       y0 ——外推点的品位或厚度值；

       y1 ——邻近外推点的实际工程的品位或厚度值；

       y2 ——邻近y1的实际工程的品位或厚度值；

       h1 ——y0与y1之间的距离（外推距离）；

       h2 ——两实际工程之间的距离；

        β ——调节系数，β一般取4；当y1远远大于y2时，β取16。

A.5 控制点品位厚度求取

       对于辅助计算点（控制点）的品位厚度值的求取，是通过周边邻近工程的品位厚度，采取距离平方反比法求取。

A.6 降维形变处理

       矿体形态千差万别，它们都处于分数维状态，矿体真实的形态不可知，若用简单几何图形和数据统计的计算，不符合对地学数据的结构地质变量的认识，要按实际形态去计算，又是不可能的。地质体是由结构地质变量构成的，地质体的空间构形可用断面表示，地质变量的空间结构也可用断面来表示。为了计算的简便化，SD法采取断面构形技术，进行降维处理，将高维变为低维，用剖面的2维反映体3维。同时，为了计算的规则化,将断面形态进行齐底“拓扑”形变，保证齐底拓扑形变后的矿体面积保持不变，保证了计算的结果的唯一性,不存在压缩的计算。而且用数学公式去描述对地质情况认识的变化，采用SD样条函数（分段连续多项式样条函数）去拟合结构地质变量，使SD法成为一种断面曲线法，使断面积分成为可能，为断面积分计算奠定了基础。同时使得SD法实现了不依据矿体形态进行计算,同时很好解决了实际中由于分支复合现象导致的矿体图形多解性的争议。因此，通过“降维形变”技术方法，使得断面积分成为可能。

A.7 矿体搜索计算

A.7.1 SD样条函数的建立，解决了结构地质变量曲线的最佳拟合问题。结构地质变量曲线拟合的效果，直接影响到断面积分结果的准确性和可靠性。因此，为了寻求最佳拟合曲线，SD创始人作了大量的研究实践，结果表明：不同的矿体的结构地质变量变化千差万别，复杂程度相差甚远，很难用其他数学曲线去拟合。为此，两位创始人经过反复研究，选择了分段连续的三次样条函数，并对其进行了必要的改造，使其既能保持三次样条函数运用的灵活性，又能让它适合各种地质变量挠度状态曲线，并丰富了三次样条曲线应用。改造的关键点是将三次样条函数与矿体复杂度T直接关联，矿体复杂度T是一个随矿体结构地质变量复杂性变化的动态量，因而三次样条曲线既适应小挠度曲线，也适应较大挠度的曲线，故而SD样条函数拟合效果较理想。因此，SD样条函数适应各种类型有序数列的数据拟合。不仅在矿产领域它能用数学公式客观地反映矿体各种复杂状态，而且在其他领域也起到了独特的作用。

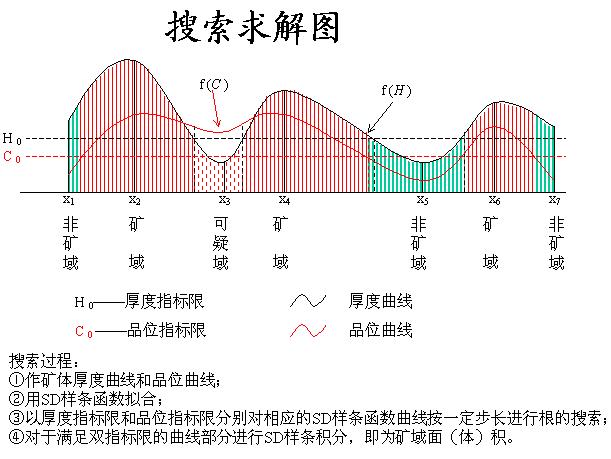
A.7.2 利用风暴品位处理后的样品，经矿体圈定后得出单工程的平均品位和厚度，经过齐底拓扑形变后，这些地质变量在断面线上构成有序的点列数据，用SD样条曲线去拟合, 建立品位和厚度的SD样条曲线。SD样条曲线拟合后，再以一定的步长插值得到各插值点的品位和厚度，并按边界品位、可采厚度、米百分值（米克吨值）去搜索，判断出断面上矿域和非矿域的范围，当品位达边界品位（或最低工业品位），而厚度未达到可采厚度的，划为可疑域，可疑域由动态百分值去判定它属矿域或非矿域,从而得到断面上矿体的面积（图A1）。这种自动按双指标在SD样条曲线上进行动态搜索确定矿域计算的资源储量结果稳定、可靠、唯一，避免了由其它方法因块段划分不同，引起的资源储量结果差异大、可靠性差等现象。

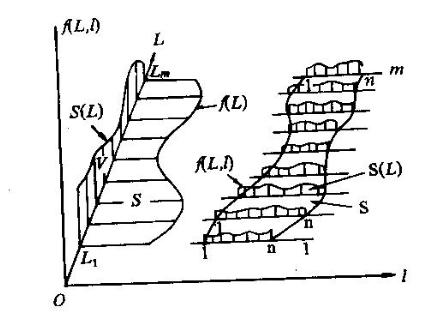
A.7.3 将断面上矿体面积，作为面结构变量，将其在垂直投影面方向上的点和数据用SD样条曲线拟合，再以一定的步长插值，用边界品位搜索得到矿体的体积。

                          (10)

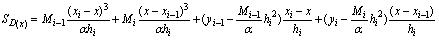
(10) 式中：

——节点x_i上对应型值点y_i值；

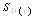
x  ——节点位置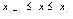；；i=2,3，…n； 

hi ——节点间距；

Mj ——型值点yi的二阶导数；

α ——修正值，；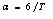

T ——复杂度。

A.7.5 SD法计算过程同时也就是动态搜索确定矿体的过程，这与几何法有所不同。SD搜索求解的实现，不仅解决了样条函数反函数求解难的问题，同时解决了合理而灵活选用工业指标的问题以及储量计算中任意划分矿块矿段灵活计算的问题，使得SD法可以适应各种需求的资源储量估算。更重要的是它实现了不依据先确定矿体形态去进行计算,也很好解决了实际中由于分支复合现象导致的矿体图形多解性的争议。

图A1 SD齐底拓扑-搜索求解图

A.7.6 搜索过程中涉及的具体计算表达式如下：

图A2 资源储量积分计算关系图

说明:

L——矿体长度方向；

I——矿体宽度方向；

m——断面线条数；

n——工程数；

D——矿石体积质量。

如图A2所示，垂直矿体铅直厚度的水平投影面（LOl）上有m条断面线，每条线上有n个工程，L为矿体长度方向，l为矿体宽度方向，矿体厚度函数为f（L,l），矿体品位和厚度乘积的函数为F（L,l），D为矿石体积质量，则：

a) 单工程平均品位 ：为各样品的品位与其计算厚度加权。

                                                                                        (11)

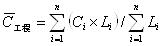
(11)式中：

 ——单工程的平均品位；

 ——各够矿或矿化样品的品位；

 ——各够矿或矿化样品的计算厚度（铅直厚度或水平厚度或真厚度）；

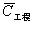
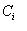
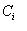
 n   ——样品个数；

b) 单工程计算厚度：为各样品计算厚度之和。

                                                                                                     (12)

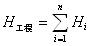
(12) 式中：

——单工程计算厚度 ；

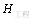
  Hi    ——各够矿或矿化样品的计算厚度；

   n    ——样品个数。

c) 矿体断面面积S（L）：

                                               (13)

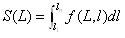
d) 矿体体积V：

                                                      (14)

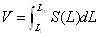
e) 矿体断面平均厚度Hs：

                                               (15)

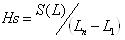
f) 体平均厚度Hv：

                                                                (16)

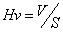
g) 矿石量Q：

                                                                  (17)

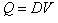
h) 面金属量Ps：

                                                (18)

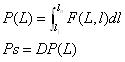
i) 体金属量P：

                                                    (19)

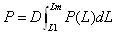
j) 面平均品位Cs：

                                                        (20)

k) 体平均品位C：

                                                                     (21)

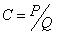
8. 伴生组分的SD法估算

在估算过程中，伴生组分无论是基本分析还是组合分析，均可与主矿种一起，采取共同搜索的方式与主矿种同时计算其量，伴生组分个数不限。伴生组分的估算及资源储量分类按有关规范执行。

9. SD精度

9.1 SD精度既是矿产资源储量精确程度的度量，又是工程控制程度的体现。递进及逼近思想，是SD精度能顺利解决资源储量可靠性的核心技术。因此，它可以作为资源储量可靠程度的度量，也可作为勘查程度划分的依据。利用SD精度，可以确定工程间距，预测工程数。有效指导勘查工作进程，减少盲目性、增强计划性。SD精度它对探矿中储量精度不可知的风险，以及对采矿中的储量可靠程度不确定的风险，提出了量化标准。用SD精度可指导勘查施工达到要求的勘查程度，控制工作程度，让探采部门自己有效控制风险，在获得最佳效益的同时，合理利用资源。

9.2 SD精度η的计算公式如下：

                                                                           (22)

(22)式中：

η——SD精度；

ρ——框架指数；

η₀——原始精度。

9.3 基距Ha是框块的基本框棱,它是工程控制程度到一定程度,被认为可以确认矿体的真态的最小框格的框棱。只要确定出基距Ha,就可得到SD预测精度。SD基距值考虑了矿床成因、矿体规模、矿种类别、工程类别、工程控制程度、矿体的复杂程度等影响资源储量估算的诸多综合因素。

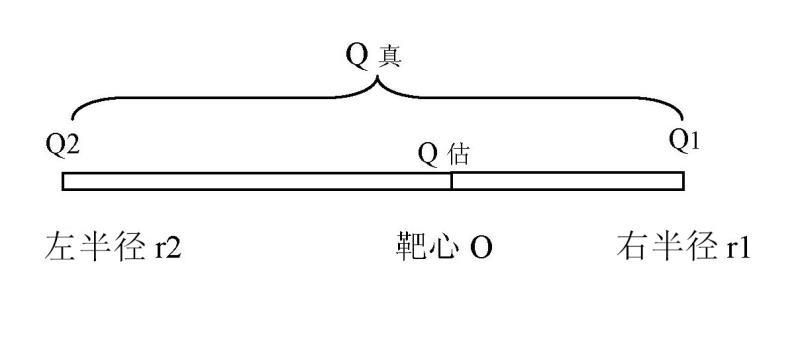
9.4 SD法通过SD精度可确定在当前工程控制下资源储量相对于真量的变化范围。用当前最佳估值乘、除精度求得真量预测靶区的端点预测值，形成用于定量控制资源储量风险的变化区间。如下图A3所示，Q_估是当前最佳估值，Q_真是真量区间，当前最佳估值 Q_估是靶区靶心O的点位，取储量预测误差r1和r2为靶区半径，直线r1r2是以靶心O为中心的不对称靶区直径。靶区直径两端点的Q1 Q2形成的预测靶区的真量区间[Q1 ,Q2] , Q1为下限值，Q2为上限值。

图A3 SD真量靶区示意图

9.5 SD精度与地质可靠程度关系应用

据SD精度与地质可靠程度关系应用图的划分（见下图A4），用SD精度基本区间和SD精度调节区间的共同部分确定的具体地质可靠程度等级区间分别为：

SD精度为  80% ≤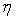≤ 100 % 表示地质可靠程度是探明的；

SD精度为  45% ≤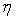＜  65 % 表示地质可靠程度是控制的；

SD精度为  15% ≤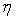＜  30 % 表示地质可靠程度是推断的；

SD精度为  2% 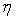 ≤＜  10 % 表示地质可靠程度是预测的。

除以上四个等级区间外，其余区间为相应的待定区间：

SD精度为  65 %≤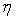＜80 % 表示地质可靠程度是探明­控制待定；

SD精度为  30 %≤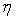＜45% 表示地质可靠程度是控制推断待定；

SD精度为  10 %≤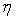＜15% 表示地质可靠程度是推断预测待定；

SD精度为   0 %≤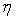＜ 2% 表示地质可靠程度是无意义的。

待定区间不属于地质可靠程度等级区间，它应结合地质研究程度，给予相应的等级确定。例如：

SD精度计算值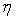为72%，其值落在“探明控制待定”区间，SD法不能直接确认是探明的，还是控制的，这要根据对地质特征，矿床特征等认识来确认，它是属于探明的等级还是控制的等级。如果简单，则归为探明的，如果复杂且不能明确确认的则归为控制的。

图A4  SD精度与地质可靠程度划分图

10. SD法优势

10.1 适用性广

SD方法及系统适用于除油气以外的其他固体矿产勘查过程中的所有阶段。

10.2 适用性强

采用通用地质勘查数据就可进行资源量估算，在可行性研究确定经济意义后，可直接估算储量。

10.3 使用简便

软件系统使用成本低，效率高，操作简单。只需将估算矿区的范围划定，输入原始数据，资源量、储量便可自动计算结果，随之自动绘制所需图件，最终自动生成报告所需文、图、表。

10.4 估算结果可信

SD软件系统资源量、储量估算结果精准、图件可视三维，估算结果可靠程度高，风险低，争议小。特有的资源量、储量区间可作为验证其他估算方法估算结果的工具。

10.5 预测勘查投入

在现有工程控制程度下，迅速划分当前资源量、储量级别，同时预测未来勘查工程数。预测几何法网度，减少盲目施工，预测投资风险，预测项目投资额度。

10.6 确定投资技术风险

根据对资源量、储量可靠性的量化值（SD精度），确定投资矿区项目资源量、储量的投资技术风险。